The universe is not a computer, but it behaves exactly like one—it processes information.

Seth Lloyd, Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos. New York: Alfred A. Knopf, 2006.

Los inicios

Computāre, en latín, viene de com + putāre (con, junto + calcular, aclarar, recortar, podar, resolver, pensar, creer, suponer, sostener). Estas diversas acepciones nos dan la pista de aquel origen en donde el concepto primordial resuena en los planteamientos de esta palabra, y cuyas ondas concéntricas del significado nos lleva a explorar más allá, mucho más, de la convención.

Se dice que el primer uso registrado de la palabra «computer», en inglés, aparece en el libro The Yong Mans Gleanin (1613), del poeta Richard Braithwaite (1588-1773).

What art thou (O Man) and from whence hadst thou thy beginning? What matter art thou made of, that thou promisest to thy selfe length of daies: or to thy posterity continuance. I haue (sic) read the truest computer of Times, and the best Arithmetician that euer (sic) breathed, and he reduceth thy dayes into a short number: The daies of Man are threescore…

[Stack Exchange]

¿Qué eres tú (oh Hombre) y de dónde tuviste tu comienzo? ¿De qué materia estás hecho, que te prometes a ti mismo una larga vida, o continuidad a tu posteridad?
He leído al más veraz calculador de los Tiempos y al mejor aritmético que jamás haya respirado, y él reduce tus días a un número breve: los días del Hombre son sesenta [años]…

(En alusión al pasaje del Salmo 90:10.) 

El término “computadora (computer)” pasó de “la persona dedicada a calcular (computer)” a la máquina electrónica que

…mediante determinados programas, permite almacenar y tratar información, y resolver problemas de diversa índole. [RAE]

Ya en lo físico. Ya con carcaza. Ya en la máquina que computa. Pero no podemos evitar el ahondar en las profundidades subterráneas de la raíz griega de máquina que está emparentada con μῆχος (mēkhos) y quiere decir remedio o recurso. Ésta también se asociaba tanto a dispositivos físicos, ¡como a estrategias calculadas!:

En la década de 1540, la palabra [máquina] se usaba para referirse a «cualquier tipo de estructura.» Proviene del francés medio machine, que significa «dispositivo, artefacto,» y este a su vez del latín machina, que se traduce como «máquina, motor, máquina de guerra; dispositivo, truco; instrumento.» Este término también dio origen al español máquina y al italiano macchina. Su raíz se encuentra en el griego makhana, una variante dórica del ático mēkhanē, que significa «dispositivo, herramienta, máquina.» Además, en griego, también podía referirse a “artificio, astucia”. [Etymoline]

En la antigua Grecia la mēkhanē, μηχανή, era también un mecanismo escénico que hacía descender a los dioses. La muy famosa expresión ἀπὸ μηχανῆς θεός (“dios desde la máquina”) deviene de:

…un mecanismo de elevación que, desde la época de Esquilo, se utilizaba para la espectacular suspensión y descenso en escena de personajes decisivos para la acción de la obra. Era una viga articulada sostenida por otra vertical giratoria. La carga se elevaba con una cuerda mediante una polea y un torno manual, guiada por el operador del mecanismo, el “mecánico” (μηχανοποιός), quien, para facilitar el manejo, equilibraba la carga con contrapesos. [Noesis]

Virgilio (70 a. C-19 a. C), en su obra La Eneida, publicada después de su muerte por instrucciones del emperador Augusto, hace una analogía entre la “machina muros” y el caballo de Troya. Recordemos el pasaje:

—”¡Oh desdichados, qué locura tan grande os posee, troyanos!
¿Creéis que los enemigos ya se han marchado?
¿Pensáis que algún regalo de los dánaos puede estar libre de engaño?
¿Así conocéis a Ulises?
O bien están escondidos los aqueos en este madero,
o esta máquina ha sido construida contra nuestros muros,
para espiar nuestras casas y caer desde lo alto sobre la ciudad,
o se oculta en ella algún ardid.
¡No confiéis en el caballo, troyanos!
Lo que sea que esto sea, temo a los griegos incluso cuando traen regalos.”

Dicho esto, lanzó con todas sus fuerzas una enorme lanza
contra el costado del monstruo y el curvo vientre ensamblado.
La lanza se clavó allí temblando, y al golpear el vientre,
resonaron las entrañas huecas y las cavernas emitieron un gemido.
Y si no hubieran sido adversos los designios de los dioses,
y no hubieran cegado nuestra razón,
él habría impulsado a destruir con el acero los escondrijos de los griegos;
Troya estaría aún en pie, y tú, alta fortaleza de Príamo, existirías todavía.

La dupla de sentido que conlleva la palabra «máquina» nos hace dudar de la verdadera existencia física de caballo. Por machina muros podríamos especular que, en realidad, se trataba de una alegoría de astucia, ingenio y artificio para adentrarse en el territorio como polizones.

Pero no sólo. En el otro lado del mundo, máquina, en chino, 机器 (jīqì), viene de 机 (jī) + 器 (qì). (Es decir, mecanismo, motor, máquina o inteligencia táctica + artefacto, dispositivo, aparato o vasija.) Interesante es saber que en el neoconfucianismo, el 理 (lǐ) es el principio o ley universal, mientras 器 (qì) es la manifestación física o concreta (la “forma” que toma ese principio en el mundo). ¿Puede el dao manifestarse en un “qì” (objeto)? ¿Son las máquinas extensiones del lǐ a través del qì?

Está máquina o plan estructurado que opera como un mecanismo oculto o como herramienta activa de la inteligencia humana es empleada por Cicerón en el sentido de «maquinar». Aún más próxima a «artilugios». Lo hace en sus obras In Catilinam y De Natura Deorum.

No sé a quién ni cómo podría engañar, ni qué podría sacar de eso,
ni qué engaño o trampa podría prepararle:
no sé absolutamente nada.
Tal es el grado en que la buena fortuna de su padre ha neutralizado
todos mis engaños, tretas y artimañas de prestidigitador.
¿Qué haré…?”

¿Y qué decir de los autómatas?, de esas máquinas asociadas al ingenio. Los autómatas han significado para la humanidad la posibilidad de crear movimiento y sentido en lo otro, en lo separado de nuestra propia condición; a veces, sólo por diversión; otras, por utilidad.

En The MAD Museum hay una vasta muestra, desde la antigüedad hasta nuestros días.

Vale la pena recordar que muchos de estos autómatas fueron primero imaginados en poemas y trazos.

El libro Autómata Old and New (1895), de Conrad William Coke (1843-1926) rastrea la historia de autómatas, de manera erudita, desde el antiguo Egipto y grecolatino, haciendo referencias a Lucian, Herodoto, Pausanias y Platón. También menciona juguetes mecánicos como los νευροσπάστα (“lo que se mueve tirando de cuerdas”) o marionetas.

Pero, quizás, toda invención surge de la imperiosa necesidad de la mente creativa por hallar metáforas. Decía Aristóteles (384 a. C.- 322 a. C.), en Poética, obra custodiada por copistas por durante un largo periodo y conservada en el mundo islámico gracias a traducciones al árabe, que metaforizar es percibir lo semejante dentro de lo desemejante, que la metáfora reescribe la realidad mediante un proceso retórico.

Lo más grande, por mucho, es ser un maestro de la metáfora. Es la única cosa que no puede aprenderse de otros; y además, es un signo de genio, ya que una buena metáfora implica una percepción intuitiva de la semejanza en lo disímil.” (…) “Metaforizar [Metaphor] consiste en dar a una cosa un nombre que pertenece a otra; esta transferencia puede hacerse del género a la especie, de la especie al género, de una especie a otra, o con base en una analogía. [Mahadoktor]

El mismo Aristóteles introduce el concepto de analogía como una relación proporcional entre categorías del ser. Así lo hizo en su obra intitulada Metafísica por Andrónico de Rodas, un editor alejandrino del siglo I a. C, quien, se dice, le puso así porque los catorce libros de este tratado venían “después de la física”.

La palabra «analogía», ἀναλογία, viene del griego ἀνά + λόγος (hacia arriba, a lo largo de, o sobre + palabra, razón, discurso, cálculo o proporción). Y, aunque parezca irrisorio, no es fácil definirla y darle finitud en la frase “Relación de semejanza entre cosas distintas”, según la RAE. —Por ello, en la Real Academia de la Lengua, se dilatan en el asunto de la abstracción.

Más adelante, con el desarrollo de la ingeniería y la física se expanden los atributos de la palabra «analógico“ e, incluso, se vuelven técnicos porque ésta, como muchas otras, es una palabra, podría decirse, transversal o híper morfológica (lógica + matemáticas + filosofía + lingüística + tecnología…) Así, con el avance del conocimiento en otras disciplinas, comienzan a diferenciarse, por ejemplo, los sistemas analógicos de los digitales:

Si me preguntan: ¿Dónde se detuvo el segundero? Yo voy a decir: En medio del segundo 15 y 16. Pero si me sigues preguntando ¿Exactamente en que segundo o milisegundo se detuvo? No voy a poder responder. Por eso es una representación o más bien es una simulación de lo que yo creo. En el caso del reloj digital, si se detiene en el segundo 15 y 16 va a aparecer en que segundo o milisegundo exactamente se detuvo. (…) Los sistemas digitales suelen ser más precisos, son de ceros y unos. [Academia de PLC]

Un sistema analógico es un reloj de manecillas, uno autómata podría ser un semáforo programado para cambiar de color. Pero, cuidado: hay autómatas analógicos, pero no todo lo digital es un autómata.

Un experto en analogías fue el filósofo, matemático, lógico, polímata, teólogo, jurista, bibliotecario y diplomático Gottfried Wilhelm Leibniz (1646-1716). La revista Memoires de l’Academie Royale des Sciences, precursora de la moderna comunidad académica internacional, publicó, en 1703, antes del bibliocidio provocado por la Revolución Francesa, en texto “Explication de l’Arithmértique Binaire”. Una obra que, aunque breve y sustancial, refleja las aspiraciones de un hombre cuyo intelecto no fue comprendido en su época.

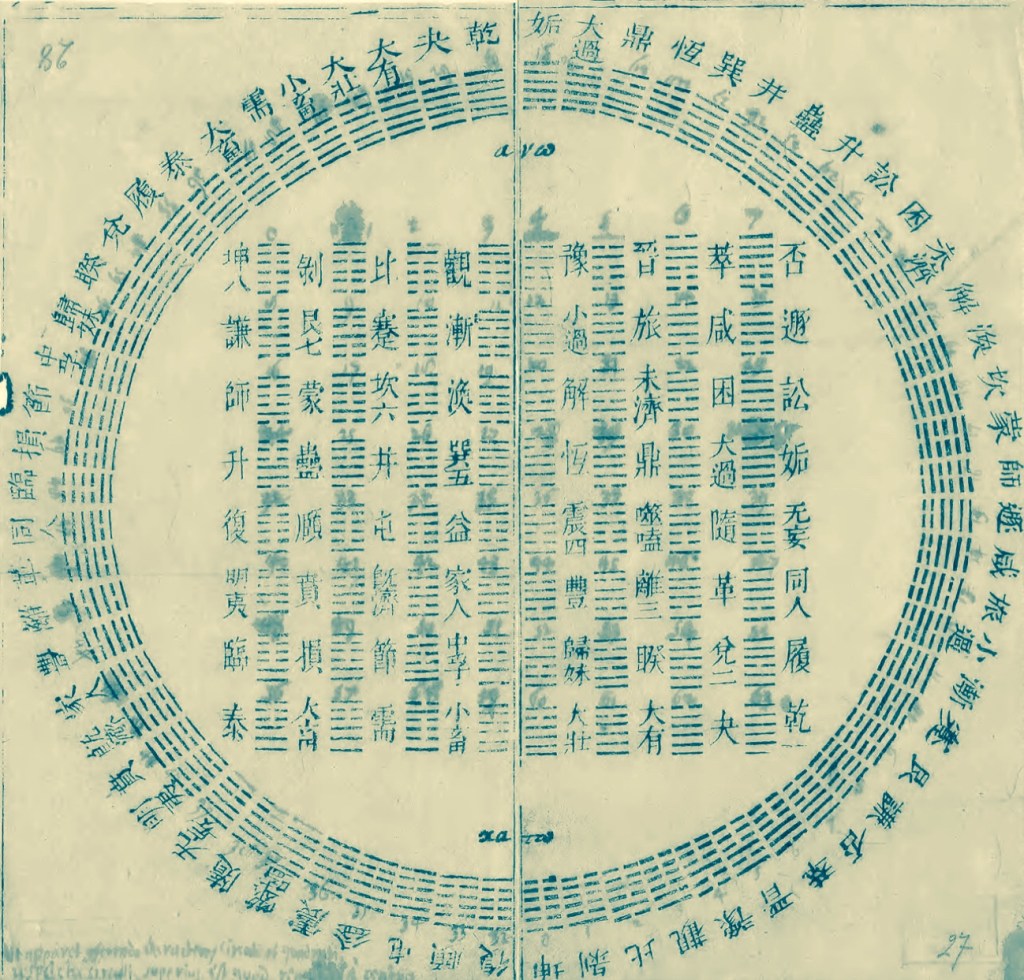
En este texto, acierta en crear una analogía junto con los hexagramas chinos del I Ching (yì jīng) en donde — (yang) y – – (ying) equivalían a 1 y 0, respectivamente.

Lo asombroso en este razonamiento es que esta aritmética de 0 y 1 resulta contener el misterio de los trazos de un antiguo rey y filósofo llamado Fuxi, quien se cree vivió hace más de 4000 años, y a quien los chinos consideran el fundador de su imperio y de sus ciencias.

El también llamado El libro de las mutaciones [o cambios], compuesto por 64 hexagramas, fue un obsequio del padre y misionero jesuita Joachim Bouvet (1656-1730) quien vivió gran parte de su edad adulta en China. Este libro atípico y más bien oracular, irradió los contornos del cómputo aritmético y escaló por dentro de la complejidad de operaciones con apariencia simple, desvelando así el muy conocido por nosotros código binario.

Los chinos perdieron el significado de la Cova o de las lineaciones de Fuxi, quizá hace más de mil años, y han escrito comentarios sobre el tema en los que han buscado no sé qué significados remotos, de modo que su verdadera explicación ahora tiene que venir de los europeos. He aquí cómo: hace poco más de dos años envié al reverendo padre Bouvet, el célebre jesuita francés que reside en Pekín, mi método de contar con 0 y 1, y no hizo falta nada más para que él reconociera que esa era la clave de las figuras de Fuxi. En una carta que me escribió el 14 de noviembre de 1701, me envió la gran figura de este príncipe filósofo, que llega hasta el número 64 y no deja lugar a dudas sobre la veracidad de nuestra interpretación, de modo que puede decirse que este padre ha descifrado el enigma de Fuxi con la ayuda de lo que le había comunicado. Y como estas figuras son quizá el monumento científico más antiguo que existe en el mundo, esta restitución de su significado, después de tan largo intervalo de tiempo, parecerá tanto más curiosa.

Esta formulación del traspase de un sistema decimal a uno binario penetró en las capas de la comprensión combinatoria. Congruente con sus inquietudes, Leibniz caminó sobre las bifurcaciones de sentido entre la física y metafísica, en la búsqueda de una “mathesis universalis” y un “alfabeto del pensamiento humano”:

Nexus una rectificanda in controversiis, ita ut simplicissime aliquis dicat: ‘Calculemus’.

En Dissertatio de arte combinatoria (1666).

Si pudiéramos reducir el razonamiento a una forma de cálculo, dos personas en disputa podrían sentarse con pluma y papel y decir ‘calculemos’.

Se ignora si Leibniz tuvo acceso a los trabajos de Thomas Harriot (1560–1621), quien entre 1604 y 1605 también registró los 1 y 0 en métodos de cálculo en manuscritos que jamás, según parece, fueron publicados. Tampoco se sabe si tuvo contacto con Juan Caramuel (1606-1682) quien sí publicó, en 1670, una primera descripción del sistema binario en su Mathesis biceps.

Muchos años después, George Boole (1815-1864) considerado uno de los fundadores de las ciencias de la computación, con formación autodidacta…

…Revolucionó la lógica al aplicar métodos del entonces emergente campo del álgebra simbólica a la lógica. Mientras que la lógica tradicional (aristotélica) se basaba en catalogar los silogismos válidos de diversas formas simples, el método de Boole ofrecía algoritmos generales en un lenguaje algebraico, aplicables a una infinidad de argumentos de complejidad arbitraria. Estos resultados aparecieron en dos obras fundamentales: The Mathematical Analysis of Logic (1847) y The Laws of Thought (1854).

Boole también escribió poemas y, como buen buscador de sentido, fue lector de clásicos. Su formación integraba los aspectos más relevantes de las humanidades. Podría decirse que Boole fue a la lógica lo que Newton a la física: Un traductor del pensamiento en ecuaciones.

En el primer capítulo de The Laws of Thought comenta:

El propósito del presente tratado es investigar las leyes fundamentales de aquellas operaciones de la mente mediante las cuales se realiza el razonamiento; expresarlas en el lenguaje simbólico de un cálculo, y sobre esta base, establecer la ciencia de la lógica y construir su método; aplicar dicho método al análisis de las formas y procesos del pensamiento humano; y finalmente, reunir a partir de los diversos elementos de verdad revelados en el transcurso de estas investigaciones algunas posibles intuiciones sobre la naturaleza y constitución de la mente humana.

Y, más adelante, en el segundo capítulo, añade:

Concibamos, entonces, un álgebra en la cual los símbolos x, y, z, etc., admitan indistintamente los valores 0 y 1, y únicamente esos valores. Las leyes, los axiomas y los procesos de tal álgebra serán, en toda su extensión, idénticos a las leyes, axiomas y procesos de una álgebra de la lógica. Sólo una diferencia de interpretación los distinguirá. Sobre este principio se establece el método de la presente obra.

Charles Sanders Peirce (1839-1914), una década después, comenzó a ampliar y sistematizar el álgebra booleana:

En “An Improvement in Boole’s Calculus of Logic” (1867), Peirce sugiere la necesidad de una mejora en la lógica booleana, no en el contexto de la lógica de predicados, sino debido a su incapacidad para expresar enunciados existenciales dentro del marco de la lógica de términos. Su artículo de 1870, “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole’s Calculus” (DNLR), revela su ambición de unir la notación algebraica de Boole con el esfuerzo de De Morgan por representar relaciones. Muchos coinciden en que este artículo introduce, por primera vez en la historia, el vocabulario esencial de la lógica de predicados de primer orden. Posteriormente, en “On the Algebra of Logic” (1880), Peirce investiga dos tipos de operaciones sobre relaciones —la suma relativa y el producto relativo—, y “The Logic of Relatives” (conocido como “Nota B”), publicado en su libro editado Studies in Logic by Members of the Johns Hopkins University (1883), muestra un avance importante en la cuantificación, influido por el trabajo de O. H. Mitchell (quien fue su alumno). Finalmente, el artículo de Peirce de 1885, “On the Algebra of Logic: A Contribution to the Philosophy of Notations”, ha sido considerado como el texto donde presenta plenamente su teoría de la cuantificación. [The Stanford Encyclopedia of Philosophy]

¿Y luego?

Hoy en día, es conocido el caso de “Las computadoras de Harvard”, un grupo de mujeres que trabajaron en el Harvard College Observatory entre lo siglos XIX y el XX. La palabra «computadoras» en este contexto no se refiere a máquinas electrónicas sino a su denominación original: “Personas que computan.” Hacían cálculos, ordenaban, resolvían, pensaban. Edward Charles Pickering (1846-1919) las contrató para trabajar como “calculadoras humanas”. Unos dicen que Pickering creía que las mujeres podían realizar cálculos meticulosos y a menor costo que los hombres; otros, que la utilidad radicaba en la novedosa inclusión de las mujeres en la ciencia. Como sea, su trabajo permitió la creación de grandes catálogos estelares como el Henry Draper Catalogue.

El hecho es que no fue sino hasta los siglos XIX y XX cuando los planteamientos en torno al uso del código binario fueron desempolvados y llevados a la mesa armable no sólo del pensamiento futuro sino también de la acción. El traslado de aquella máquina lógica a la forma de lo físico fue lento; sin embargo, una vez que ocurrió, lo cambió todo.

Claude Shannon (1916-2001) demostró la implementación de la lógica booleana en circuitos eléctricos y relés en su tesis de maestría “A Symbolic Analysis of Relay and Switching Circuits” (1937). Se le conoce como el fundador de la teoría de la información. En su artículo “A Mathematical Theory of Communication” (1948), introdujo los conceptos de bit, entropía de la información, ruido, canal y codificación, redundancia y eficiencia. Es decir, dio origen a la era digital. Sin Shannon, tendríamos electricidad, pero no computadoras. Comunicación, pero no Internet. Relés, pero no lógica programable.

Las tres palabras clave para comprender los avances en el funcionamiento de las computadoras son «relés», «válvulas“ y «transistores.”

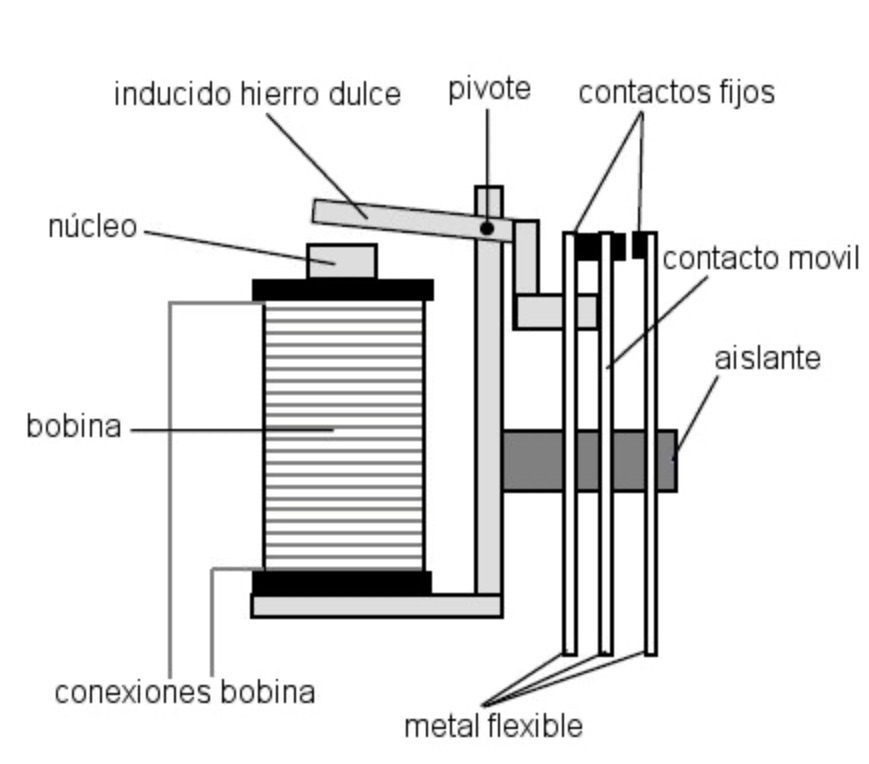
«Relés»

-Dispositivos electromecánicos que funcionan como interruptores controlados por una corriente eléctrica. Esto conecta o desconecta un circuito (1 y 0).

-Joseph Henry desarrolló el principio en 1835.

-Samuel Morse los usó en el telégrafo en 1837.

-Shannon demostró cómo podían realizar operaciones booleanas en 1937.

«Válvulas electrónicas» (tubos de vacío)

-Dispositivos electrónicos que controlan el flujo de electrones en un vacío dentro de un tubo de vidrio. Su funcionalidad es ampliar e interrumpirquie. Se usaron en las primeras computadoras electrónicas, como la ENIAC.

-John Ambrose Fleming inventó el diodo de vacío en 1904.

-Lee De Forest añadió la rejilla de control para crear el triado en 1906.

«Transistores»

-Dispositivos semiconductores (de silicio, germanio) que permiten tanto la amplificación como la interrupción a una alta velocidad (GHz) y con eficiencia energética.

-John Bardeen, William Shockey y Walter Brattain los inventaron en los laboratorios Bell en 1947. Recibieron el Premio Nobel de Física en 1956.

-Son la base de los chips modernos y de los circuitos integrados.

La influencia de Shannon en John von Neumann (1903-1957), Howard Aiken (1900-1973), Alan Turing (1912-1954) y otros dio lugar al diseño de máquinas computacionales con lógica binaria.

¿Y «computadora»?

Una definición más amplia es la de The National Institute of Standars and Tecnology (NIST):

Una máquina (real o virtual) para realizar cálculos de forma automática, que incluye, pero no se limita a, computadoras, servidores, routers, switches, etcétera. / Unidad funcional capaz de realizar cálculos sustanciales, incluyendo numerosas operaciones aritméticas y lógicas, sin intervención humana. / Un dispositivo de cómputo puede consistir en una unidad independiente o en varias unidades interconectadas. / También puede ser un dispositivo que proporcione un conjunto específico de funciones, como un teléfono o un organizador personal, o funciones más generales, como una computadora portátil o de escritorio. [NIST]

Las primeras computadoras

Z3 (1941) | Relés | Cinta perforada. Creador: Konrad Zuse (1910-1995).

Harvard Mark I (1944) | Relés y mecanismos | Cinta perforada {Construida en Harvard en colaboración con IBM} Líder del proyecto: Howard H. Aiken (1900-1973).

ENIAC (1945) | Válvulas | Reconfiguración manual
Creadores: John Presper Eckert (1919-1995) y John William Mauchly (1907-1980). {Financiada por el ejército de EE.UU en la Universidad de Pensilvania}

EDVAC (1949) | Válvulas y memoria | Programa almacenado. Continuación de la ENIAC.

UNIVAC (1951) Válvulas | Cinta magnética
Fue el primer modelo estadounidense que se vendió, principalmente a grandes instituciones. (46 unidades.)

IBM 650 (1954) | Memoria de tambor magnético. Primera computadora producida en masa. (Aproximadamente, 2000 unidades.)

Fue hasta la década de los 70 cuando la Altamira 8800 (1975) fue accesible para algunas personas; los modelos Apple II (1977) y el IBM PC (1981) lo fueron aún más.

En los años 90, fue más común el adquirir una PC así.

Hasta aquí ha sido un resumen de una larga lista de versiones de computadoras. A la fecha, cualquiera puede armar o adquirir una PC con altas capacidades, así como el elegir las características de portabilidad más aptas para su uso. No parece indispensable el detallar los ingredientes de una máquina ultra funcional. Pero sí, lo siguiente.

Como al mundo le gusta eso de mencionar a las mujeres, agrupándolas, aquí van algunas que alimentaron el interior del hardware:

• Ada Lovelace (1815-1852) es considerada la primera programadora de la historia. Trabajó junto con Charles Babage (1791-1871), quien diseñó la máquina analítica. Ella escribió el primer algoritmo para ser procesado por una máquina, anticipando la idea de que las computadoras podrían manipular no sólo números sino también símbolos y música.
• Grace Murray Hopper (1906-1992) participó tanto en el desarrollo de la Mark I como en las siguientes. Inventó el primer compilador en 1952, un programa que traduce instrucciones escritas en lenguaje humano a lenguaje máquina. También desarrolló el lenguaje de programación COBOL.
• Hedwing Eva María Kiesler (1914-2000) fue actriz de Hollywood e inventora autodidacta. Junto con el compositor George Antheil (1900-1959) patentó un sistema de comunicación por salto de frecuencia para evitar interferencia en señales de torpedos guiados por radio. Este invento fue el precursor de tecnologías como el Wi-Fi, Bluetooth y GPS.
• Katherine Johnson (1918-2020) calculó trayectorias de vuelo para las misiones Mercury, Apolo y el transbordador espacial. Fue una de las “computadoras humanas.”
• Margaret Hamilton (1936-) fue líder del equipo de ingeniería de software del MIT para el programa Apolo de la NASA. Diseñó el Software de navegación y control que permitió que Apolo 11 aterrizara con éxito en la Luna en 1969.
• Radia Perlman (1951-) es llamada “la madre de Internet”. inventora del STP (Spanning Tree Protocol) que permite que las redes complejas eviten bucles.

Más allá también están las supercomputadoras y minicomputadoras… Lo cual pone en cuestión el Principio Landauer que, según su formulador, Rolf Landauer (1927-1999), la información es física y no puede ser manipulada sin consecuencias termodinámicas. En 1961, publicó “Irreversibility and Heat Generation in the Computing Process”, en IBM Journal of Research and Development. Allí estableció el vínculo directo entre la lógica irreversible (borrar un bit) y la disipación de energía en forma de calor.

En el reciente artículo de la revista Cluster Computing, “Evolution of computing energy efficiency: Koomey’s law revisited”, publicado en octubre de 2024, sus autores proyectan:

Para que el consumo energético de las tecnologías de la información y la comunicación sea sostenible, la eficiencia energética de los sistemas de cómputo debe crecer al menos al mismo ritmo que la demanda de servicios de cómputo. Por ello, es crucial comprender cómo está evolucionando dicha eficiencia energética y cuál será su tendencia en el futuro, con el fin de tomar las medidas adecuadas cuando sea posible. Este artículo analiza la evolución de este parámetro mediante el estudio de computadoras de alto rendimiento entre 2008 y 2023, contrastando los resultados con los de la Ley de Koomey. Se concluye, tras comparar ambos conjuntos de datos, que en el periodo estudiado y en el futuro próximo, la eficiencia energética continúa creciendo exponencialmente, pero a un ritmo más lento que el establecido por la Ley de Koomey (la eficiencia energética máxima se duplica cada 2.29 años, en lugar de cada 1.57 años). Otro resultado interesante es que la eficiencia energética crece a un ritmo más lento (duplicándose cada 2.29 años) que el rendimiento computacional (que se duplica cada 1.85 años).

En este otro artículo “Landauer’s Principle: Past, Present and Future“, publicado hace tres meses en la revista Entropy, su autor cuestiona:

El rápido desarrollo de las computadoras ha generado un creciente interés por los fundamentos físicos de la computación. Este interés surge tanto de los aspectos aplicados como de los fundamentales del proceso computacional [1]. Se ha planteado la hipótesis de que todo el universo puede ser considerado como una gran computadora cuántica [2]. Cum grano salis (tomándolo con reserva), incluso la evolución natural puede verse como un proceso de computación que explota las propiedades físicas de los materiales [3]. En su sentido más general, la computación implica transformar entradas en salidas mediante un conjunto específico de instrucciones; nosotros restringimos nuestro enfoque al marco físico: una computadora digital se ve como un dispositivo físico que procesa bits al cambiar unidades lógicas entre estados “encendido” y “apagado”; esos cambios físicos son la computación [4]. Una pregunta razonable que se deriva de esto es ¿cuáles son las limitaciones físicas de la computación? Es decir, ¿cuál es el costo mínimo de energía para computar y cuál es la máxima velocidad posible de cálculo?

El alemán Konrad Zuse, destacado por culminar la primer computadora, la Z3 y por diseñar la primer computadora comercial, la Z4, que vendió a la Escuela Politécnica Federal de Zúrich (ETH Zürich), en Suiza, escribió en The Calculating Space (1969), escribió:

Mientras reflexionaba sobre la causalidad, de pronto se me ocurrió que el universo podía concebirse como una gigantesca máquina de computación. Tenía en mente la calculadora de relés: estas contienen cadenas de relés. Cuando se activa un relé, el impulso se propaga a través de toda la cadena. Pensé que eso debía de ser también como se propaga un cuanto de luz. La idea se asentó firmemente; con los años la desarrollé en el concepto del Rechnender Raum o ‘universo computante’. Sin embargo, habrían de pasar otros treinta años antes de que lograra formular correctamente la idea.

Ahora, podríamos preguntarnos, si el universo es una gran computadora, ¿de qué se alimenta? ¿Cómo opera la irreversibilidad en él? ¿El Todo es indeterminado? ¿Dónde guarda el tiempo? ¿En qué espacio escribe sus memorias?

Y, a todo esto, ¿qué digo, además, yo?

Un sombrero colgado 
es víspera espumosa que sostiene 
un futuro de a pie, 
una huella soleada, 
pero también al hueco en su presencia.